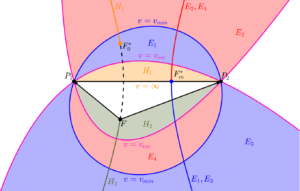
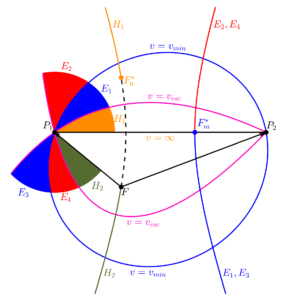
A particularly cool thing in preliminary orbit design is something called ‘Lambert’s Problem’. The problem consists of finding all of the trajectories around a central body (F) patching points P1and P2. The points are points in space, but can also be at two completely different times (in which case you have a setup that allows you to find trajectories between moving points, such as objects on two different orbits around the Earth, or interplanetary trajectories between two planets in the solar system). The very neat feature of this boundary value problem is that it has a set of solutions that can be gotten at entirely via geometric analysis. Briefly, for any given two points in space, there exists a hyperbola representing the locus of the vacant focus of the transfer trajectory (the central body is at the filled focus). The location of the vacant focus uniquely defines the transfer orbit, and can result in an infinite number of elliptical transfers (each of which actually represents two different transfers as the ellipse can be followed the short way or the long way), and infinite number of hyperbolic transfers, two unique parabolic transfers, and a unique (elliptical) minimum energy transfer, whose vacant focus lies on the line joining the two points in space. Kaplan (in his 1976 textbook) classified the families of trajectories as E1-E4 (where E1/E3 were the short/long ways on one set of ellipses and E4/E2 were the short/long ways on another set of ellipses, and H1-H2 (the two hyperbolic families). He also showed how each family corresponds to a unique branch of the hyperbola of vacant foci locations, which encodes the possible departure directions of each family. The figure to the left is directly based on one in Kaplan’s text. One limitation of this representation, however, is that it does not clearly show the bounding action of the parabolae on the long-way ellipse families. We can fix this by extending the figure and shading the entire loci of all transfers, as shown below:
